机器学习,周志华 P28-37
目的
如何评估一个学习算法在test集的泛化能力,提高学习算法的预测能力。对于不同问题要有具体的性能评估方法。
回归问题
1. mean squared error(均方误差)
$$
E(f;D)=\frac{1}{m}\sum^{m}_{i=1}(f(x_i)-y_i)^2
$$
2. 数据分布D,概率密度p(x),均方误差为:
$$
E(f;D)=\int_{x\sim D}(f(x)-y)^2p(x)dx
$$
分类问题
1. error rate and accuracy
indicator function
$$
I(\cdot) \in {0,1}
$$
离散
对样本D,分类错误率:
$$
E(f;D)=\frac{1}{m} \sum^{m}{i=1} I(f(x_i)\neq y_i)
$$
精度定义:
$$
\begin{aligned}
acc(f;D) &= \frac{1}{m}\sum^{m}{i=1}I(f(x_i)= y_i) \
&= 1-E(f;D)
\end{aligned}
$$
数据分布D,概率密度函数p(x)
对样本D,分类错误率:
$$
E(f;D)=\int_{x\sim D}I(f(x)\neq y) p(x)dx
$$
精度定义:
$$
\begin{aligned}
acc(f;D) &=\int_{x\sim D}I(f(x)= y)p(x)dx \
&=1-E(f;D)
\end{aligned}
$$
2. confusion matrix
| 真实情况 | 预测结果pos | 预测结果neg |
|---|---|---|
| positive | True Positive | False Negative |
| negative | False Positive | True Negative |
precision rate
$$
P=\frac{TP}{TP+FP}
$$
recall rate
$$
R=\frac{TP}{TP+FN}
$$
model select
- 多个训练模型所形成的P-R曲线,如果一个学习器的P-R曲线被另一个学习器的P-R曲线完全包住,则断言后者性能优于前者。
- P-R曲线所形成的面积,比较难计算
- precision rate 与 recall rate 是互相矛盾的。”平衡点”BEP(Break-Even Point)是度量学习器优劣的一种方法,即 precision rate == recall rate时的值。
3. F1 - measure
$$
F1 = \frac{2\times P \times R}{P + R}
= \frac{2\times TP}{m+TP-TN}
$$
其中,m样本总数.
对于某些应用,对precision与recall的重视程度不同,F1度量一般形式:
$$
F_{\beta}=\frac{(1+\beta^2)\times P \times R}{(\beta^2\times P)+R}
$$
β>0;其中,β>1 recall 有更大影响; β<1 precision 有更大影响。
多个二分类confusion matrix(混淆矩阵)
多次训练/测试;多个测试集训练/测试;多分类任务,每两两类别组合形成一个混淆矩阵。
$$
\begin{aligned}
macro{-}P &= \frac{1}{n}\sum_{i=1}^nP_i \
macro{-}R &= \frac{1}{n}\sum_{i=1}^nR_i \
macro{-}F1 &= \frac{2\times macro{-}P \times macro{-}R}{macro{-}P + macro{-}R}
\end{aligned}
$$
或,将各混淆矩阵的对应元素进行平均
$$
\begin{aligned}
micro{-}P &= \frac{\overline{TP}} {\overline{TP}+\overline{FP}} \
micro{-}R &= \frac{\overline{TP}} {\overline{TP}+\overline{FN}} \
micro-F1 &= \frac{2\times micro{-}P \times micro{-}R} {micro{-}P + micro{-}R}
\end{aligned}
$$
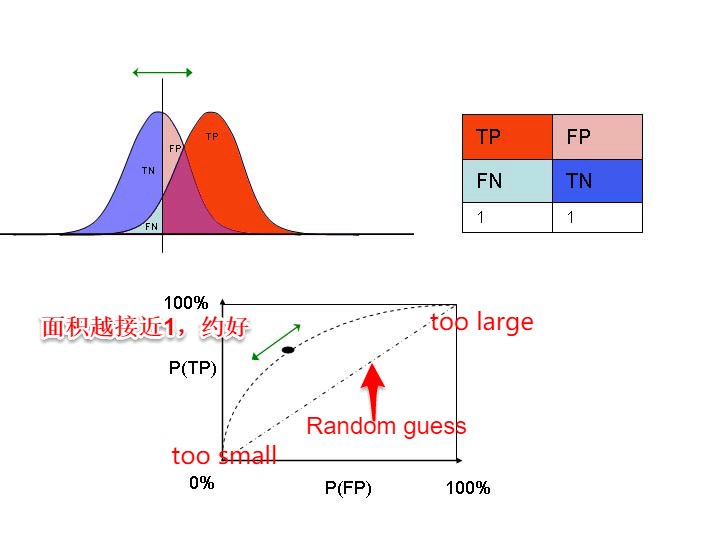
3. ROC 与 AUC (Area Under ROC Curve)
ROC(Receiver Operating Characteristic)曲线: 纵坐标TPR(True Positive Rate),即recall Rate ; 横坐标FPR(False Positive Rate).
$$
\begin{aligned}
{TPR} &=\frac{TP}{TP+FN} \
FPR &=\frac{FP}{TN+FP}
\end{aligned}
$$
AUC 即ROC曲线下的面积,假定ROC曲线是由{(x_1,y_1),…,(x_m,y_m)} 点组成,AUC可估算为:
$$
AUC = \frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_i)(y_{i+1}+y_i)
$$
给定m个正例,n个反例,则排序“LOSS”定义:
$$
\ell_{rank}=\frac{1}{m \times n} \sum_{x^+ \in D^+}\sum_{x^- \in D^-}(I(f(x^+)<f(x^-))+\frac{1}{2}I(f(x^+)=f(x^-)))
$$
存在以下关系:
$$
AUC = 1 - \ell_{rank}
$$
4. cost-sensitive error rate and cost curve
相关文献
在不同应用中,对不同类型分类产生的错误所占比重不同,cost-sensitive(代价敏感) error rate:
$$
E(f;D;cost)=\frac{1}{m}(\sum_{x_i \in D^+} I(f(x_i) \neq y_i) \times cost_0)
+\sum_{x_i \in D^-} I(f(x_i) \neq y_i) \times cost_1)
$$
在非均等代价下,ROC曲线不能直接反应出学习器的期望总体代价,而cost curve(代价曲线)则可达到目的。
横轴是取值[0,1]的正例概率代价:
$$
P(+)cost = \frac{p \times cost_0}{p \times cost_0 + (1-p) \times cost_1}
$$
其中,p为样本中正例概率(TPR);
纵轴是取值[0,1]的归一化代价:
$$
cost_{norm} = \frac{FNR \times p \times cost_0 + FPR \times (1-p) \times cost_1}{p \times cost_0 + (1-p) \times cost_1}
$$
其中,假反例率FNR=1-TPR。
曲线绘制方法:ROC曲线上每一点对应了代价平面上的一条线段,设ROC曲线上的坐标为(TPR,FPR),计算对应的FNR,然后在代价平面绘制(0,FPR) 到 (1,FNR)线段。所有线段之下的公有面积即所有条件下学习器的期望总体代价。